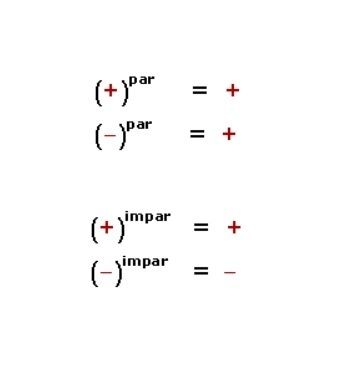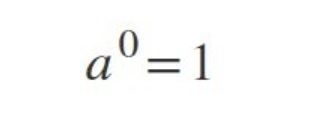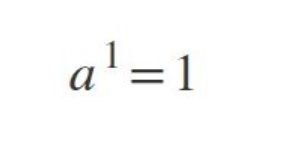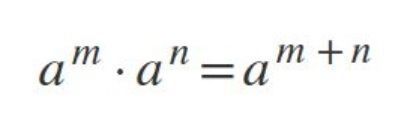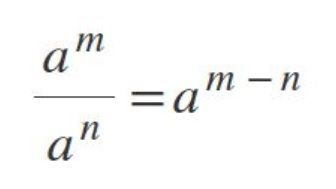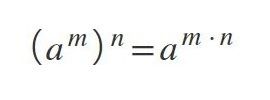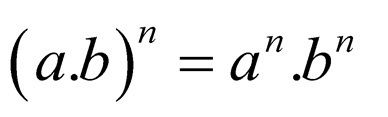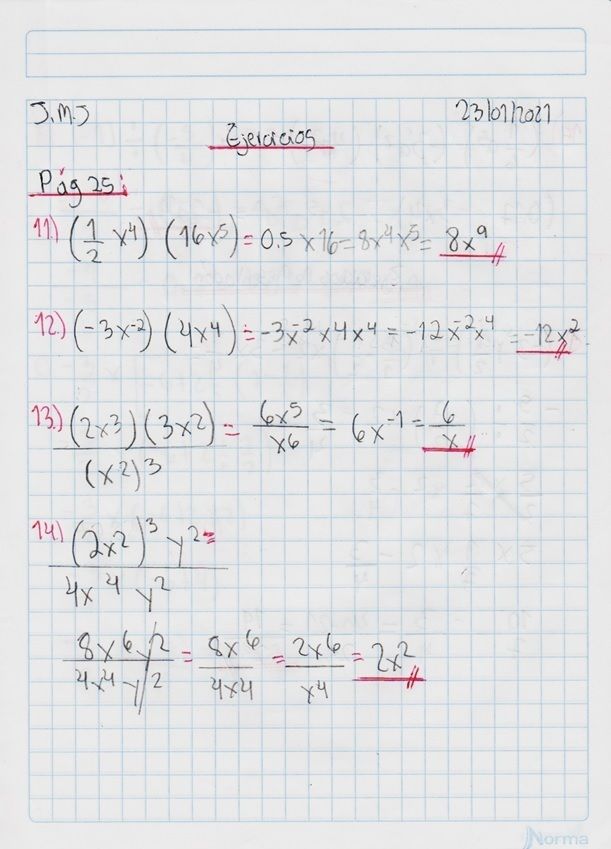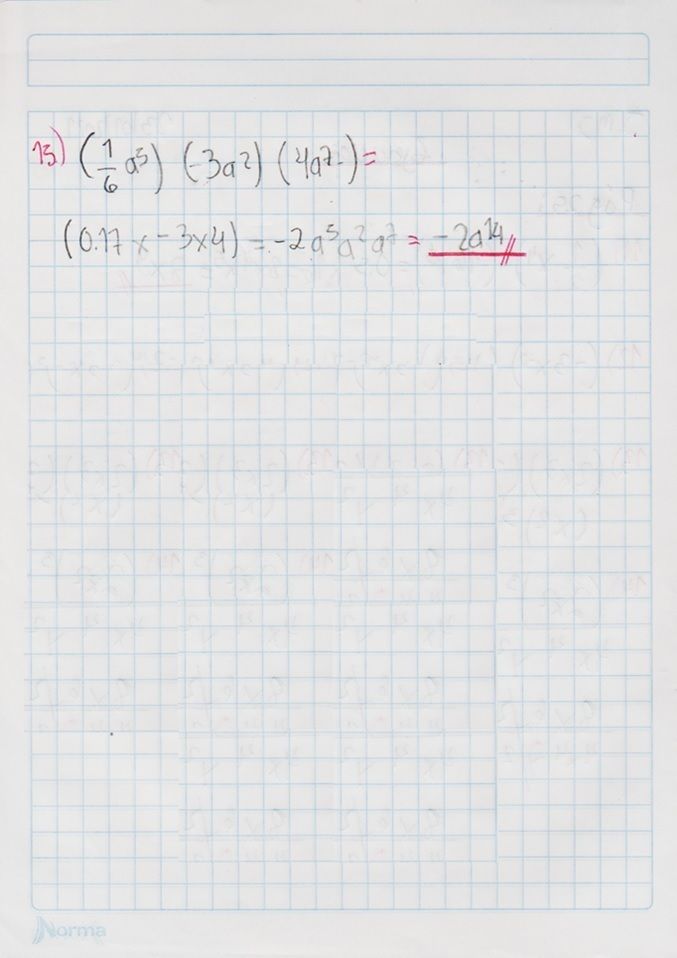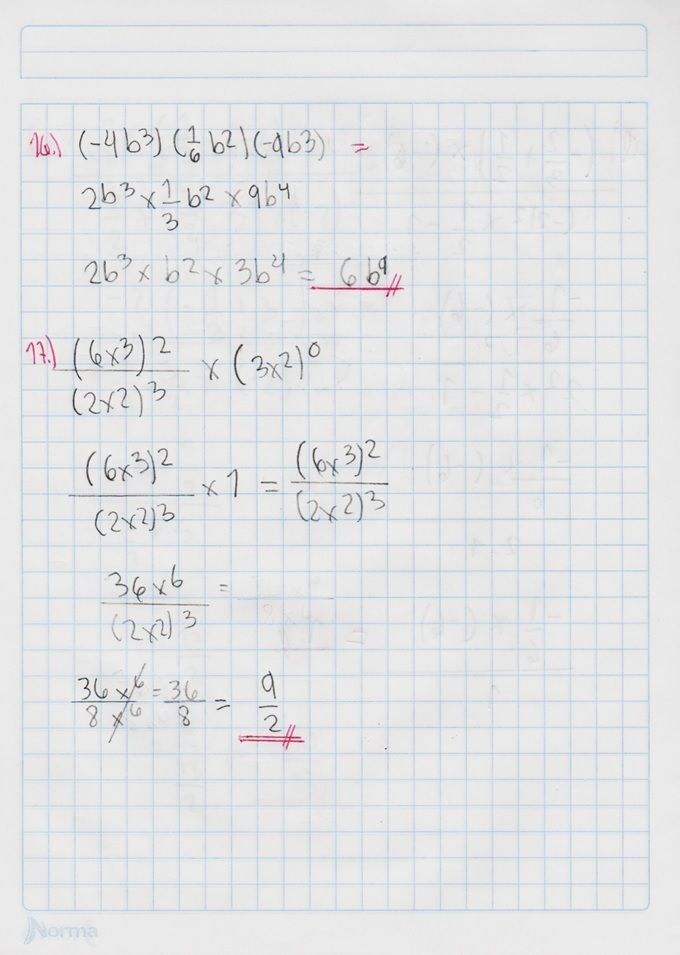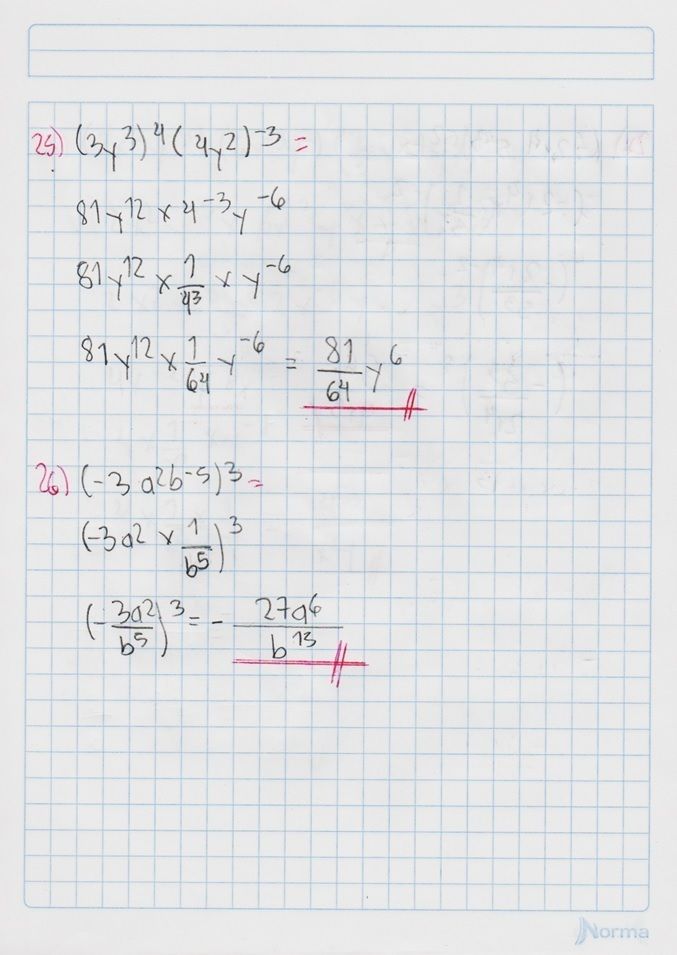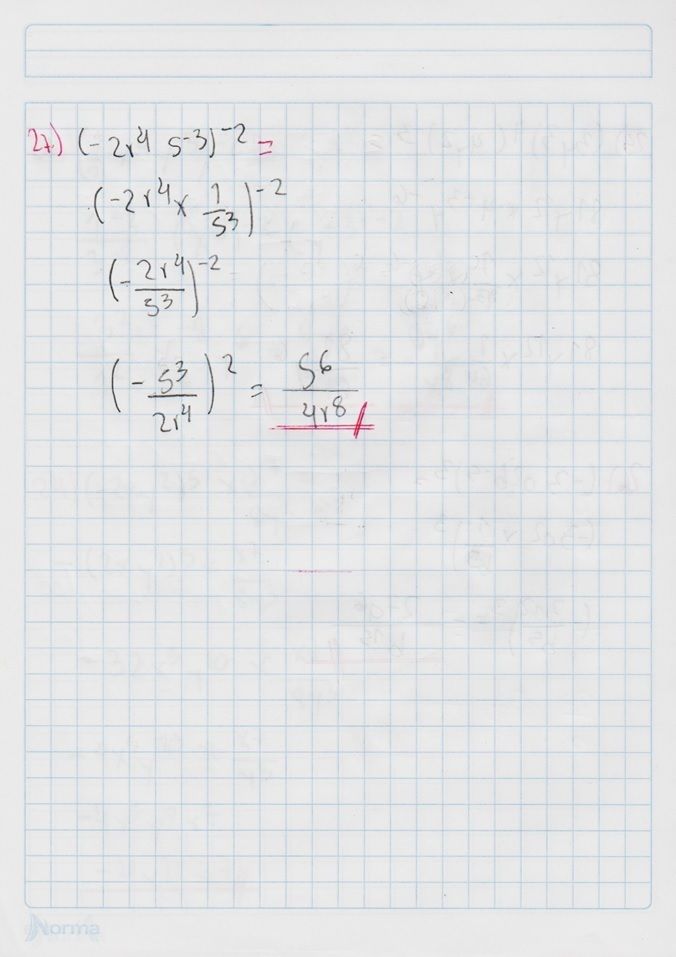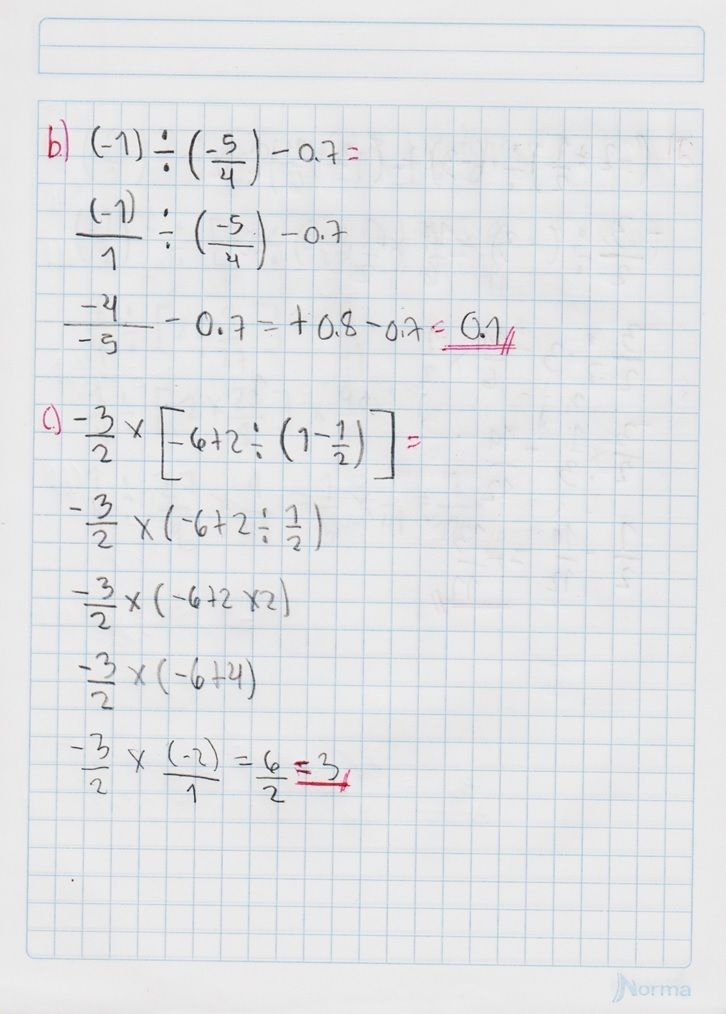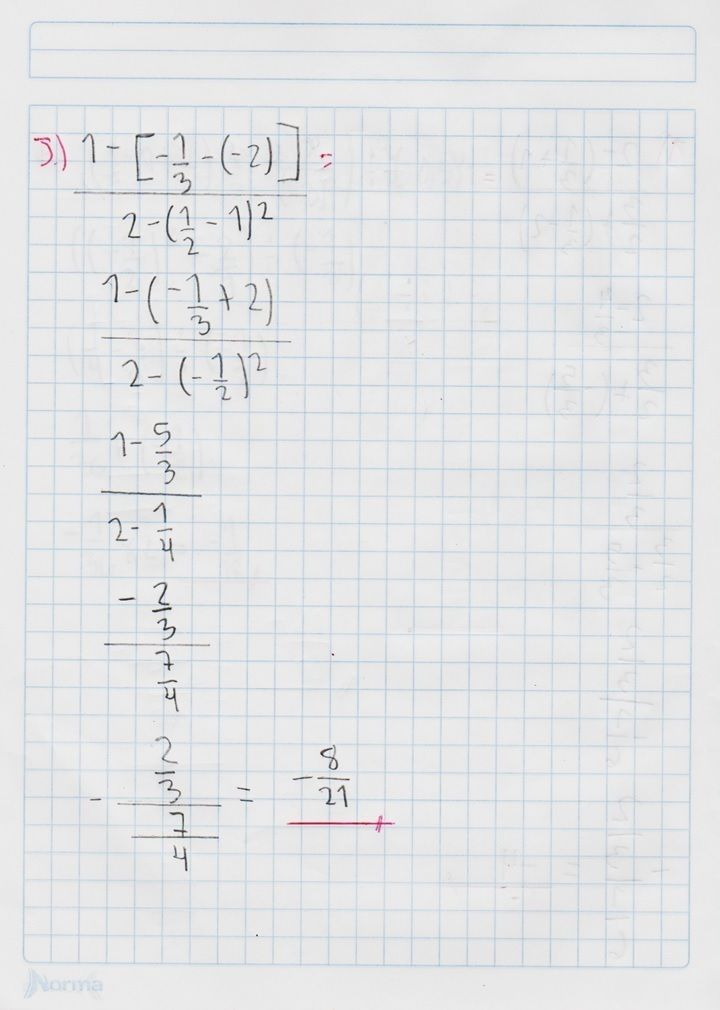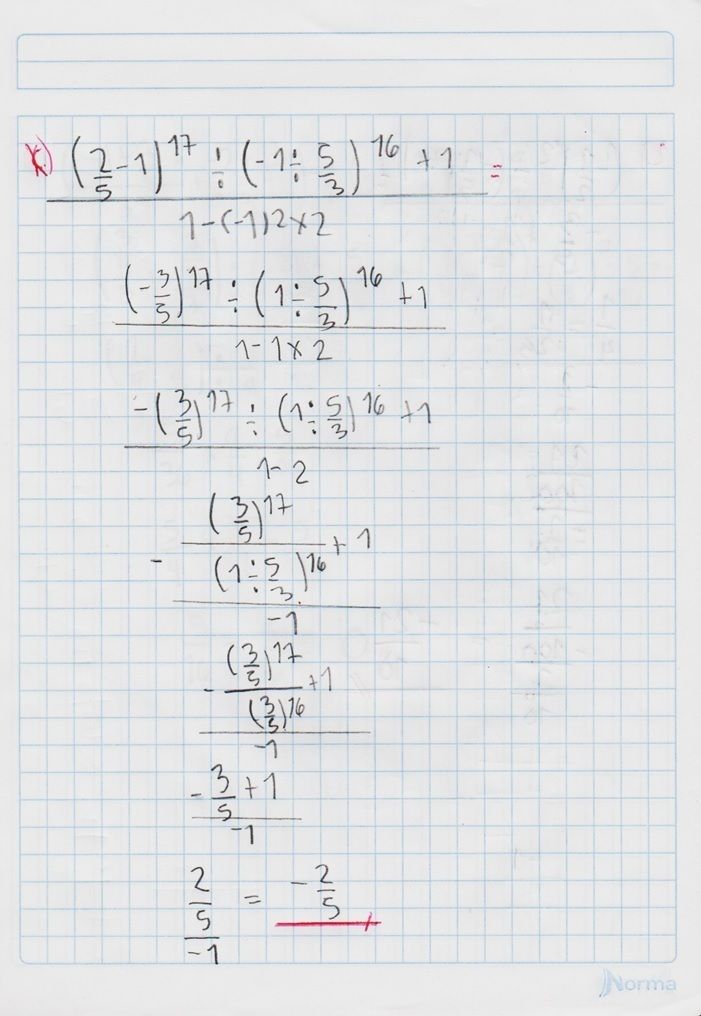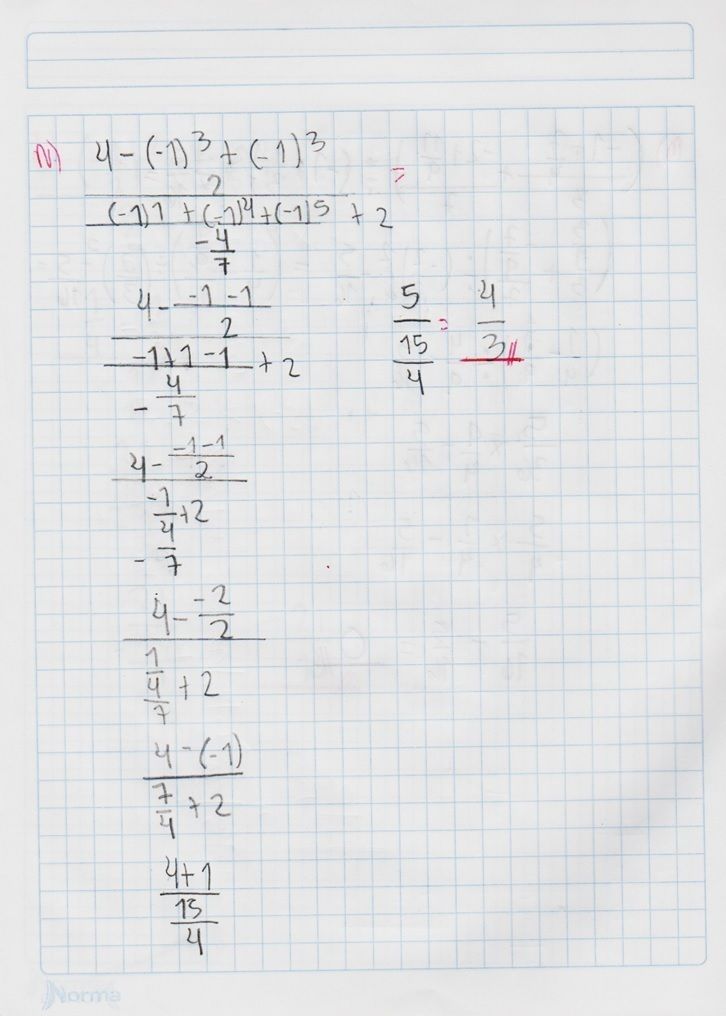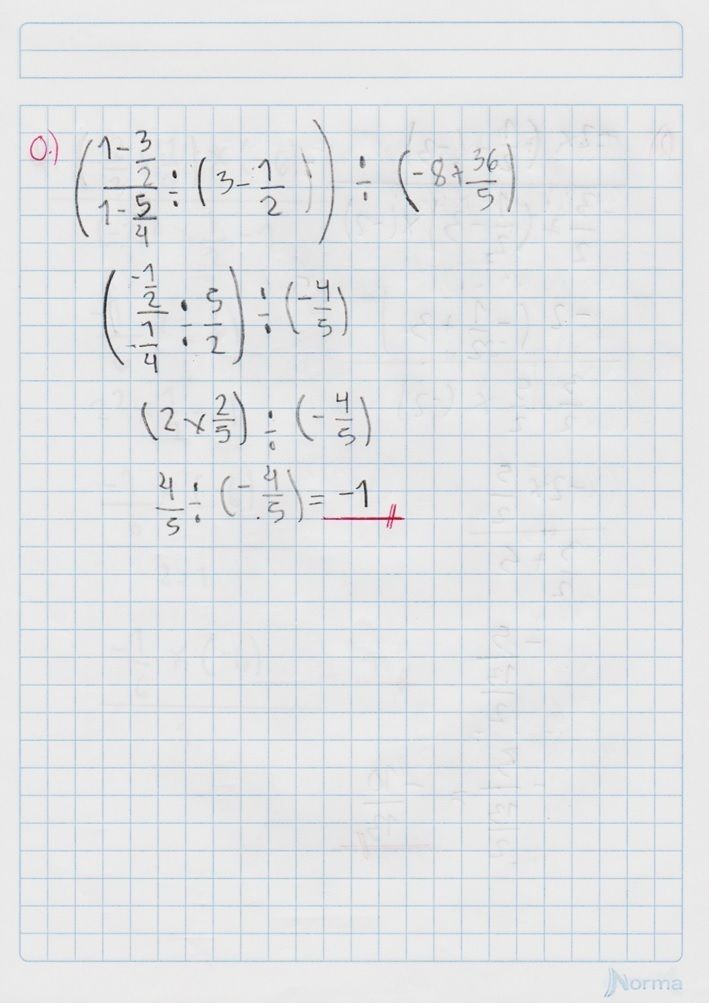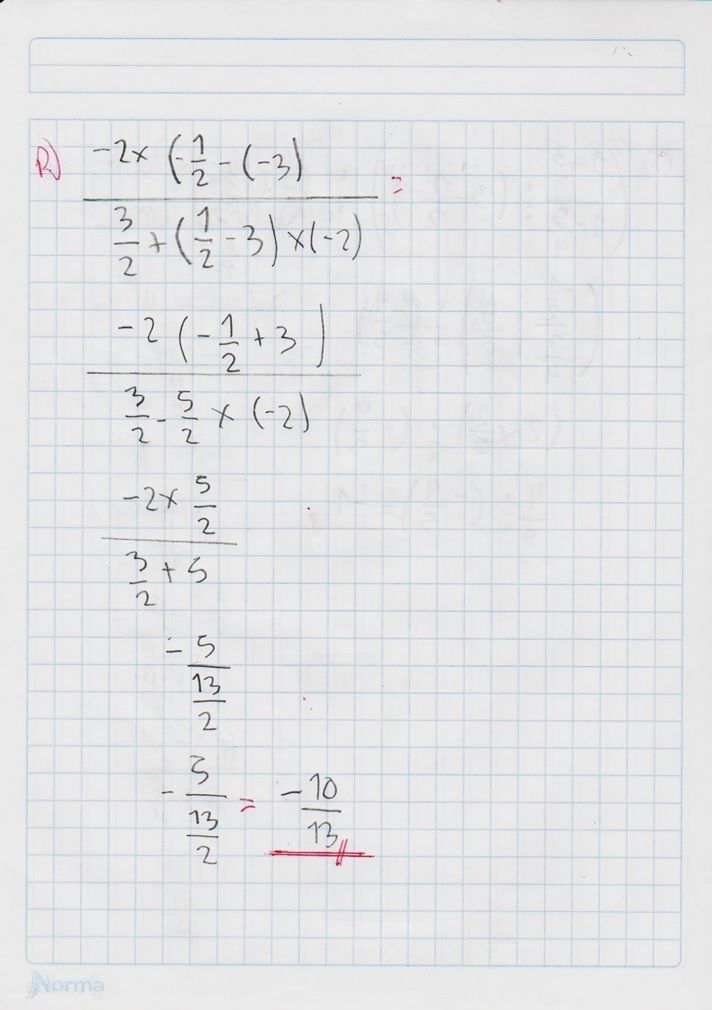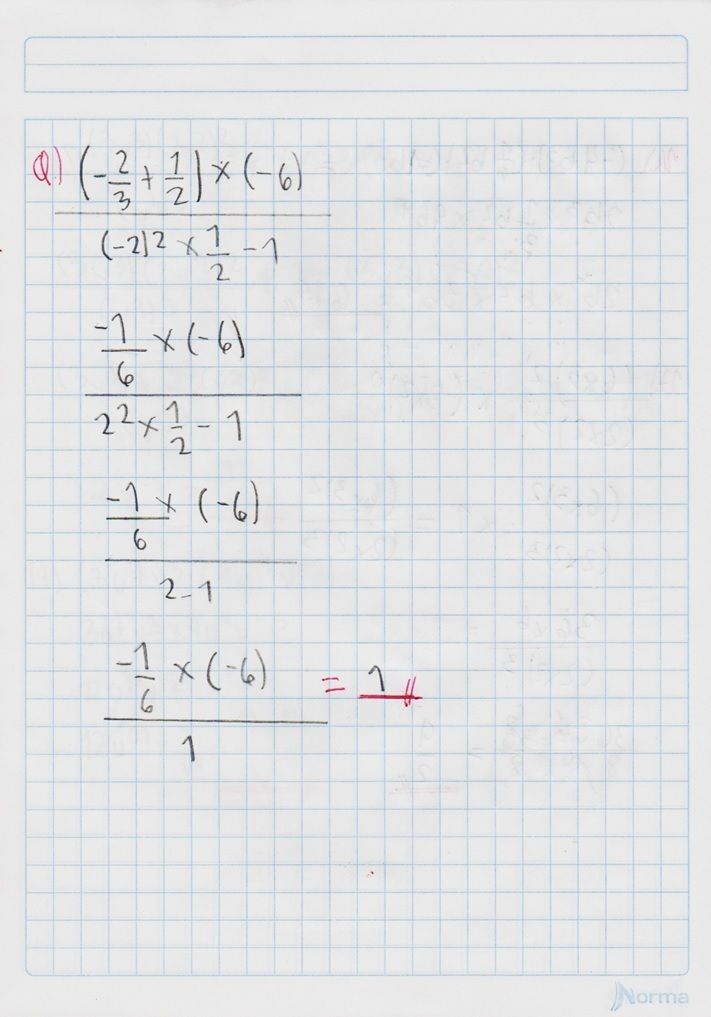José Carlos Rodríguez Mejía 4to. BACO "B"
Pinned to
2753
1
0
GoConqr Review
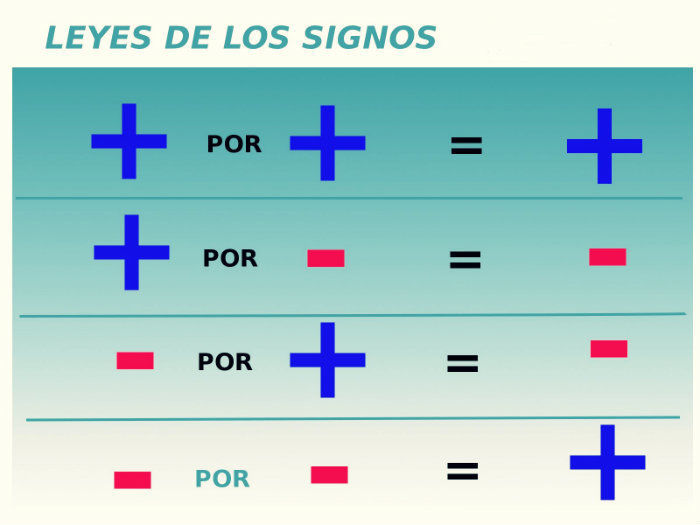
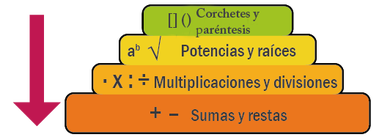
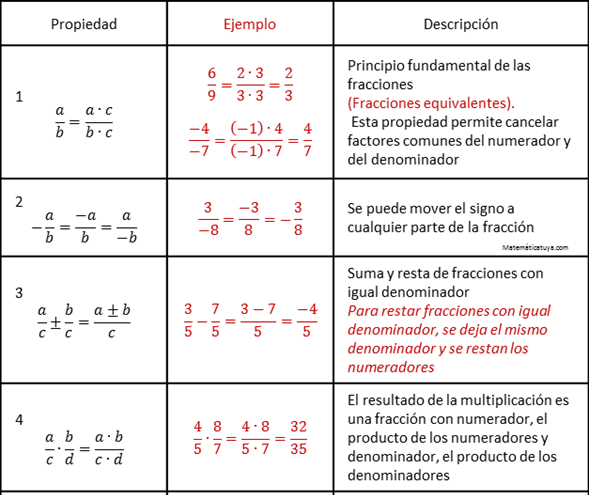
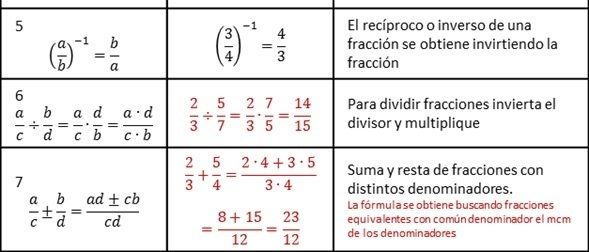
Conoce qué son y como actúan la ley de signos, las leyes de los exponentes, las jerarquías de las operaciones y propiedades de las fracciones, con este conjunto de diapositivas.
No tags specified
|
|
Created by José Carlos Rodríguez Mejía
about 4 years ago
|
|
Rate this resource by clicking on the stars below:




 (0)
(0)
Ratings (0)
| 0 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| 0 |
0 comments
There are no comments, be the first and leave one below:
Close